DMS Tutorial - Evaluation of generated models

Evaluation of models (discovered knowledge)

Strategies for estimating a true error-rate of a classifier (model)

The true error rate is statistically defined as the error rate of the classifier on an asymptotically large number of new cases that converge in the limit to the actual population distribution. An empirical error rate can be defined as the ratio of the number of errors to the number of cases examined.

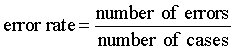
If we were given an unlimited number of cases, the true error rate would be readily computed as the number of samples approached infinity. In the real-world applications, the number of samples available is always finite, and typically relatively small. The major question is then whether it is possible to extrapolate from empirical error rates calculated from small sample results to the true error rate.

There are a number of ways of presenting sample cases to the classifier to get better estimates of the true error rate. Some techniques are much better than others. In statistical terms, some estimators of the true error rate are considered biased. They tend to estimate too low, on the optimistic side, or too high, on the pessimistic side. We will briefly review the techniques that give the best estimates of the true error rate, and consider some of the factors that can produce poor estimates of performance.

Training set and Test set error rate estimates

The quality of a classifier is determined by its ability to correctly predict classifications for unseen examples. The classifier must be evaluated with a set of examples that is separate from the training set of samples used to build it. The set of examples used to evaluate classifier is called test set.

The training set error rate of a classifier is the error rate of the classifier on the sample cases that were used to build the classifier, i.e. training set. The training set error rate is also known as the re-substitution or reclassification error rate. Figure 1 illustrates the relationship between the apparent error rate and the true error rate.

Figure 1: Training set error rate versus true error rate

Since we are trying to extrapolate performance from a finite sample of cases, the training set error rate is the obvious starting point in estimating the performance of a classifier on new cases. With an unlimited design sample used for learning, the apparent error rate will itself become the true error rate eventually. However, in the real world, we usually have relatively small sample sizes to design a classifier and extrapolate its performance to new cases. For most types of classifiers, the training set error rate is a poor estimator of future performance. In general, training set error rates tend to be biased optimistically. The true error rate is almost allways much higher than the training set error rate. This happens when the classifier has been over-fitted (over-specialized) to the particular characteristics of the sample data.

Over-fitting

It is useless to design a classifier that does well on the design sample data, but does poorly on new cases. Using only the training set error rate to estimate future performance of a classifier can often lead to disastrous results on new data.

The nature of this problem, is called over-fitting of the classifier to the data. Basing our estimates of performance on the training set error rate leads to similar problems. The extent to which classification methods are susceptible to over-fitting varies. Many unexperienced modellers have been deceived by the mirage of favorably low training set error rates. Fortunately, there are techniques for providing better estimates of the true error rate.

Since at the limit with large numbers of cases, the training set error rate does become the true error rate, we can raise the question of how many design cases are needed for one to be confident that the training set error rate effectively becomes the true error rate. There are very effective techniques for guaranteeing good properties in the estimates of a true error rate even for a small sample. While these techniques measure the performance of a classifier, they do not guarantee that the training set error rate is close to the true error rate for a given application.

Estimation of the classifier true error rate

Training set error rates alone are sometimes used to report classifier performance, but such reports can often be ascribed to factors such as a lack of familiarity with the appropriate statistical error rate estimation techniques or to the computational complexities of proper error estimation.

Randomness - prerequisite for true error rate determination

The requirement for any model of honest error estimation, i.e., for estimating the true error rate, is that the sample data are a random sample. This means that the samples should not be pre-selected in any way, or that the modeller should not make any decisions about selecting representative samples.

The concept of randomness is very important in obtaining a good estimate of the true error rate. A computer-based data mining system is always at the mercy of the design samples supplied to it. Without a random sample, the error rate estimates can be compromised, or alternatively they will apply to a different population than intended.

Randomness, which is essential for almost all empirical techniques for error rate estimation, can be produced most effectively by a computer.

Train-and-Test Error Rate Estimation

For a real problem, one is given a sample from a single population, and the task is to estimate the true error rate for that population - not for all possible populations. This type of analysis requires far fewer cases, because only a single, albeit unknown, population distribution is considered. Moreover, instead of using all the cases to estimate the true error rate, the cases can be partitioned into two groups, some used for designing the classifier, and some for testing the classifier. While this form of analysis gives no guarantees of performance on all possible distributions, it yields an estimate of the true error rate for the population being considered. It may not guarantee that the error rate is small, but the number of test cases needed is surprisingly small. In the next section, we consider this train-and-test paradigm for estimating the true error rate.

It is not hard to see why, with a limited number of samples available for both learning and estimating performance, we should want to split our sample into two groups. One group is called the training set and the other the test set. These are illustrated in Figure 3. The training set is used to design the classifier, and the test set is used strictly for testing. If we hold out the test cases and only look at them after the classifier design is completed, then we have a direct procedural correspondence to the task of determining the error rate on new cases. The error rate of the classifier on the test cases is called the test sample error rate.

Figure 3: Train-and-test samples

Naturally, the two sets of cases should be random samples from some population. In addition, the cases in the two sample sets should be independent. By independent, we mean that there is no relationship among them other than that they are samples from the same population. To ensure that the samples are independent, they might be gathered at different times or by different investigators. A very broad question was posed regarding the number of cases that must be in the sample to guarantee equivalent performance in the future. No prior assumptions were made about the true population distribution. It turns out that the results are not very satisfying because huge numbers of cases are needed. However, if independent training and testing sets are used, very strong practical results are known. With this representation, we can pose the following question: how many test cases are needed for the test sample error rate to be essentially the true error rate?

The answer is: a surprisingly small number. Moreover, based on the test sample size, we know how far off the test sample estimate can be. Figure 4 plots the relationship between the predicted error rate, i.e., test sample error rate, and the likely highest possible true error rate for various test sample sizes. These are 95onfidence intervals, so that there is no more than a 5hance that the error rate exceeds the stated limit. For example, for 50 test cases and a test sample error rate of 0%, there is still a good chance that the true error rate is as high as 10%, while for 1000 test cases the true error rate is almost certainly below 1%. These results are not conjectured, but were derived from basic probability and statistical considerations. Regardless of the true population distribution, the accuracy of error rate estimates for a specific classifier on independent, and randomly drawn, test samples is governed by the binomial distribution. Thus we see that the quality of the test sample estimate is directly dependent on the number of test cases. When the test sample size reaches 1000, the estimates are extremely accurate. At size 5000, the test sample estimate is virtually identical to the true error rate. There is no guarantee that a classifier with a low error rate on the training set will do well on the test set, but a sufficiently large test set will definitelly provide accurate performance measures.

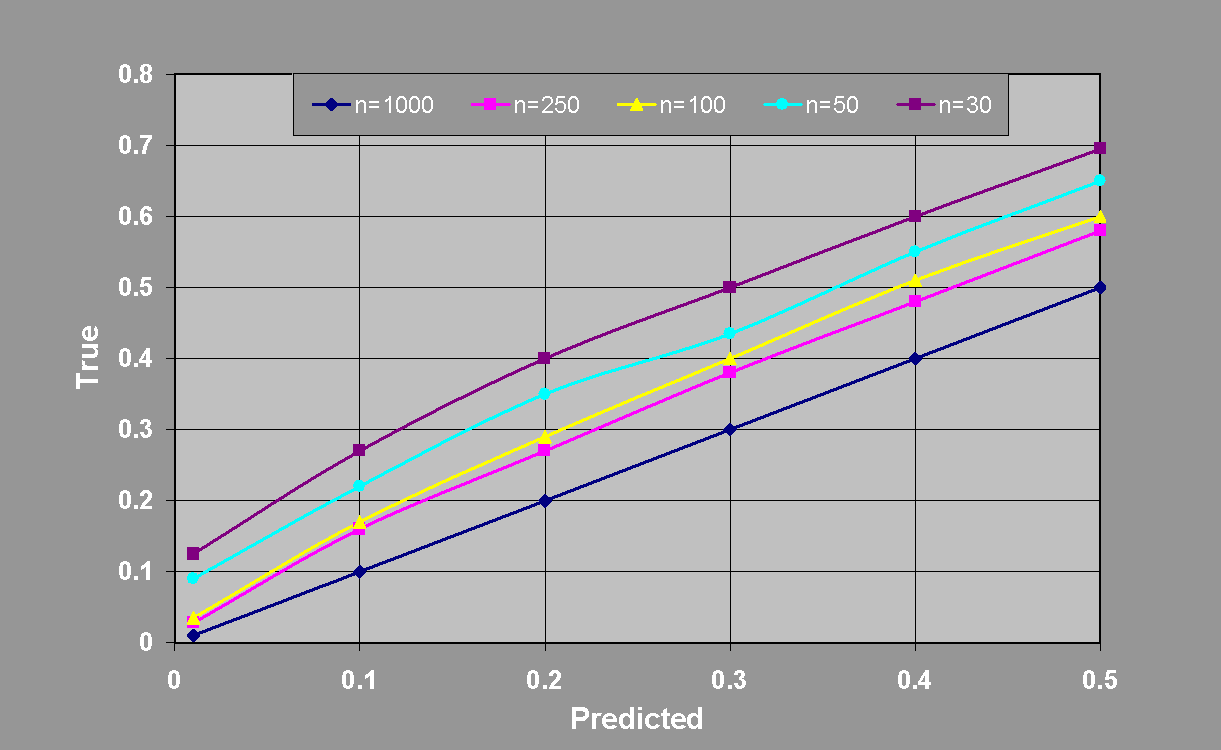
Figure 4: Number of test cases needed for prediction

While sufficient test cases are the key to accurate error estimation, adequate training cases in the design of a classifier are also of great importance. Given a sample set of cases, common practice is to randomly divide the cases into train-and-test sets. While humans would have a hard time randomly dividing the cases and excising their knowledge of the case characteristics, the computer can easily divide the cases (almost) completely randomly.

The obvious question is how many cases should go into each group? Traditionally, for a single application of the train-and-test method - otherwise known as the holdout method - a fixed percentage of cases is used for training and the remainder for testing. The usual proportion is approximately a 2/3 and 1/3 split. Clearly, with insufficient cases, classifier design is defficient, so the majority is usually used for training.

Resampling methods provide better estimates of the true error rate. These methods are variations of the train-and-test method and will be discussed next.