DMS Tutorial - Evaluation of generated models

Evaluation of models (discovered knowledge)

Evaluation of discovered knowledge or models is the key component of the modelling process for making the real progress in data mining. Depending on the problem at hand, different methods of evaluation are sought and applied. Since classification is the most common data mining problem type (many of other data mining problem types can be transformed into a classification problem type), and DMS rule induction system is designed to generate models through solving the classification problem, we will concentrate our discussion here on evaluation measures for classifier models.

Simple evaluation measures for evaluation of classification models

Crucial term for evaluation of classifiers is an error. Simply, an error is a misclassification: the classifier is presented a case, and it classifies the case incorrectly. If all errors are of equal importance, a single-error rate (error rate=number of errors/number of examples), summarizes the overall performance of a classifier. However, for many applications, distinctions among different types of errors turn out to be important. For example, the error committed in diagnosing someone as healthy when one has a life-threatening illness (known as a false negative decision) is usually considered far more serious than the opposite type of error-of diagnosing someone as ill when one is in fact healthy (known as a false positive).

If distinguishing among error types is important, then a confusion matrix can be used to lay out the different errors. Table 1 is an example of such a matrix for three classes.

True Class

Predicted Class

1

2

3

1

30

1

0

2

1

43

5

3

0

2

75

Table 1: Sample confusion matrix for three classes

The confusion matrix lists the correct classification against the predicted classification for each class. The number of correct predictions for each class falls along the diagonal of the matrix. All other numbers are the number of errors for a particular type of misclassification error. For example, class 2 in Table 1 is correctly classified 43 times, but is erroneously classified as class 3 two times. Two-class classification problems are most common, since multi-class problems can also be represented as a series of two-class problems (DMS rule induction system works in this manner, too). With just two classes, the choices are structured to predict the occurrence or non-occurrence of a single event or hypothesis. In this situation, the two possible errors are frequently given the names mentioned earlier from the medical context: false positives or false negatives. Table 2 lists the four possibilities, where a specific prediction rule is invoked.

	Class Positive (C+)	Class Negative (C-)
Prediction Positive (R+)	True Positives (TP)	False Positives (FP)
Prediction Negative (R-)	False Negatives (FN)	True Negatives (TN)

Table 2: Confusion matrix for a two-class classification problem

A classic metric for reporting performance of machine learning algorithms is predictive accuracy.

Accuracy reflects the overall correctness of the classifier and the overall error rate is (1 - accuracy). If both types of errors, i.e., false positives and false negatives, are not treated equally, a more detailed breakdown of the other error rates becomes necessary.

Accuracy has many disadvantages as a measure. These are its basic shortcomings:

It ignores differences between error types
It is strongly dependent on the class distribution (prevalence) in the dataset rather than the characteristics of examples

In medical diagnostic test evaluation, more common metrics for evaluation are sensitivity and specificity. Sensitivity is the accuracy among positive instances and specificity among negative. Sensitivity and specificity overcome negative sides of accuracy (error type resolution and condition prevalence). Using the notation in the Table 2 sensitivitiy and specificity can be expressed as:

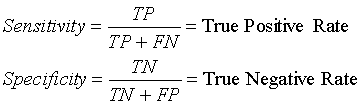
In the evaluation of information retrieval systems, the most widely used performance measures are recall and precision.

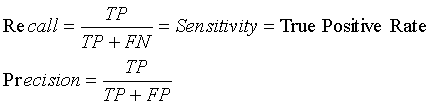
Recall and precision are mostly utilized in situations where TP is small when compared with TN.

In some fields, such as medicine, where statistical hypothesis testing techniques are frequently used, performance is usually measured by computing frequency ratios derived from the numbers in Table 2. These are illustrated in Table 3. For example, some test may have a high sensitivity in diagnosing an illness (defined as its ability to correctly classify patients that actually have the disease), but may have poor specificity if many healthy people are also diagnosed as having that illness (yielding a low ratio of true negatives to overall negative cases). These measures are technically correctness rates, so the error rates are one minus the correctness rates.

Sensitivity	TP / C+
Specificity	TN / C-
Predictive value (+)	TP / R+
Predictive value (-)	TN / R-
Accuracy	(TP + TN) / ((C+) + (C-))

Table 3: Formal measures of classification performance