DMS Tutorial - Evaluation of generated models

Evaluation of models (discovered knowledge)

ROC Analysis

Sensitivity and Specificity describe the true performance with greater clarity than accuracy, but they also have disadvantages. For a particular classifier they represent two measures, one for the positive cases and the other one for negative. A compound measure for the classifier is given through ROC - Receiver Operating Characteristic analysis. ROC is a classic methodology from signal detection theory.

Crucial for understanding ROC is a confidence thresholds in the classification task. For the strict threshold the sensitivity will be low while specificity very high. If the criterion for the threshold is lowered specificity will fall while sensitivity will raise. In this way we can compare two classifiers over a broad range of threshold conditions. ROC curve is created by plotting the true positive rate against false positive rates or sensitivity against (1-specificity). The ROC curve going along the diagonal from bottom left to upper right, represents pure-chance performance. Perfect classifier would follow left and upper axes. Real classifiers lie in between these two cases (i.e. upper left triangle of the graph).

Figure: ROC Curve

Modifying error rates: misclassification costs

The primary measure of performance that is used are error rates. There are, however, a number of alternatives, extensions, and variations possible on the error rate theme.

A natural alternative to an error rate is a misclassification cost. Instead of designing a classifier to minimize error rates, the goal would be to minimize misclassification costs. A misclassification cost is simply a number that is assigned as a penalty for making a particular type of a mistake. For example, in the two-class situation, a cost of one might be assigned to a false positive error, and a cost of two to a false negative error. An average cost of misclassification can be obtained by weighing each of the costs by the respective error rate. Computationally this means that errors are converted into costs by multiplying an error by its misclassification cost.

Any confusion matrix has n² entries, where n is the number of classes. On the diagonal lie the correct classifications with the off-diagonal entries containing the various cross-classification errors. If we assign a cost to each type of error or misclassification, the total cost of misclassification is most directly computed as the sum of the costs for each error. If all misclassifications are assigned a cost of l then the total cost is given by the number of errors and the average cost per decision is the error rate.

By raising or lowering the cost of a misclassification, we are biasing decisions in different directions, as if there were more or fewer cases in a given class. Formally, for any confusion matrix, if E_ij is the number of errors entered in the confusion matrix and C_ij is the cost for that type misclassification, the total cost of misclassification is given by the equation below:

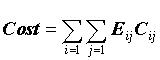
We have so far considered the costs of misclassifications, but not the potential for expected gains arising from correct classification. In risk analysis or decision analysis, both costs (or losses) and benefits (gains) are used to evaluate the performance of a classifier. A rational objective of the classifier is to maximize gains. The expected gain or loss is the difference between the gains for correct classifications and losses for incorrect classifications.

In economic analysis utility theory is employed, which allows modification of risks by a function. The nature of this function is part of the specification of the problem and is defined before the classification problem is derived

In all these cases decisions are based on modified error rates so as to measure classifier performance in units typical for the problem domain, and also provide means for making more correct decissions.