DMS Tutorial - Neural networks

Neural Networks

Neural networks or artificial neural networks (ANN), are densely interconnected networks of simple computational elements. The elements of networks are called neurons.

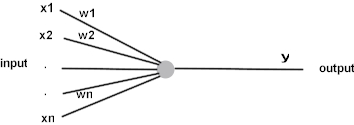
Figure 1: Neuron, a computational element of artificial neural network

The input to neuron consists of a number of values x1,x2, ...,xn, while output is single value y. Both input and output values are having continuous values, usually in the range (0,1). The neuron computes the weighted sum of its inputs, subtracts some threshold T, and passes the result to a non-linear function f, .e.g. sigmoid

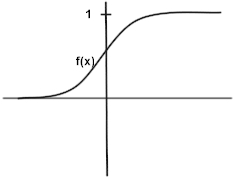
Figure2: Sigmoid function

Each element in he ANN computes the following:

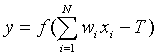
where w_i are the weights. Outputs of some neurons are connected to inputs of other neurons. In a multi-layer perceptron topology (there are many different ANN topologies), neurons are grouped into distinct layers as depicted in Figure 3.Output of each layer is connected to input of nodes in the following layer. Inputs of the first layer (input layer) are the inputs to the network, while the outputs of the last layer, form the output of the network.

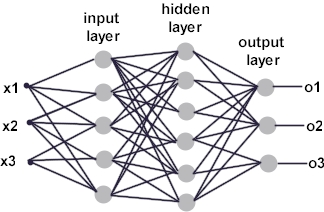
Figure 3: Multilayer perceptron

A multi-layer perceptron is especially useful for approximating a classification function that maps input vector (x₁,x₂, ... x_n) to one or more classes C₁,C₂,...C_m._. By optimizing weights and thresholds for all nodes, the network can represent a wide range of classification functions. Optimizing the weights can be done by supervised learning, where the network learns from the large number of examples. Examples are usually provided one at a time. For each example the actual vector is computed and compared to the desired output. Then, weights and thresholds are adjusted, proportional to their contribution to the error made at the respective output. One of the most used methods is the back-propagation method, in which in the iterative manner, the errors are propagated (error = the difference between desired output and the output of actual ANN) into the lower layers, to be used for the adaptation of weights.

When to apply neural nets ?

Neural nets perform very well on difficult, non-linear domains, where it becomes more and more difficult to use Decision trees, or Rule induction systems, which cut the space of examples parallel to attribute axes. They also perform slightly better on noisy domains.

One of disadvantages in using Neural nets for data mining, is a slow learning process, compared top for example Decision trees. This difference can very easily be several orders of magnitude (100-10000).

Another disadvantage is that neural networks do not give explicit knowledge

representation in the form of rules, or some other easily interpretable form. The model is implicit, hidden in the network structure and optimized weights, between the nodes.

Links to online Neural network tutorials

An introduction to neural networks
by A. Blais and D. Mertz
http://www-106.ibm.com/developerworks/linux/library/l-neural/?open&l=805,t=grl,p=NeuralNets

Neural networks
by C. Stergiou and D. Siganos
http://www.doc.ic.ac.uk/~nd/surprise_96/journal/vol4/cs11/report.html

Neural nets overview
by J. Fröhlich
http://rfhs8012.fh-regensburg.de/~saj39122/jfroehl/diplom/e-13.html

Mini-tutorial on artificial neural networks
by S. L. Thaler
http://www.imagination-engines.com/ann.htm

Artificial neural networks
by F. Rodriguez
http://www.gc.ssr.upm.es/inves/neural/ann1/anntutorial.html